Bei der Segmentierung der
Bézierkurve können an den Segmentgrenzen verschiedene
Kontinuitätsbedingungen eingehalten
werden. Im folgenden werden die beiden Kurvensegmente 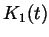 (mit den Stützpunkten
(mit den Stützpunkten 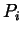 ) und
) und 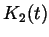 (
(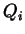 )
betrachtet, jeweils mit einem eigenen Parameterintervall (
)
betrachtet, jeweils mit einem eigenen Parameterintervall (
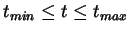 ):
):
- Lokale Kontinuität [
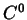 -Kontinuität]:
-Kontinuität]:
Gilt, wenn
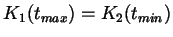 , d.h. der letzte Stützpunkt der ersten Bézier-Kurve
trifft auf den ersten Stützpunkt der zweiten Bézier-Kurve.
, d.h. der letzte Stützpunkt der ersten Bézier-Kurve
trifft auf den ersten Stützpunkt der zweiten Bézier-Kurve.
- Tangentiale Kontinuität:
- parametrisch [
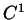 -Kontinuität]:
-Kontinuität]:
Ist gegeben, wenn 1.
und zusätzlich
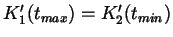 gilt. Für
Bézier-Kurven bedeutet dies:
gilt. Für
Bézier-Kurven bedeutet dies:
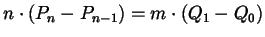 .
.
Bei zwei Bézier-Kurven gleichen Grades
folgt daraus, dass 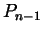 ,
, 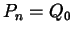 und
und 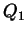 kollinear und die Abstände von
kollinear und die Abstände von 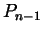 und
und 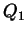 zu
zu
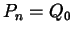 gleich sein müssen.
gleich sein müssen.
- geometrisch [
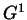 -Kontinuität]:
-Kontinuität]:
Zusätzlich zu 1. muss
gelten:
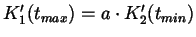 ,
, 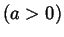 ,
,
d.h. bei Bézier-Kurven gilt: 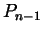 ,
, 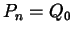 und
und
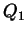 sind kollinear.
sind kollinear.
- Krümmungskontinuität:
- parametrisch [
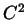 -Kontinuität]:
-Kontinuität]:
Erreicht man, wenn
zusätzlich zu 1. und 2.1. gilt:
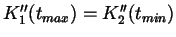 , d.h. bei Bézier-Kurven gilt:
, d.h. bei Bézier-Kurven gilt:
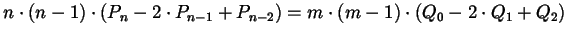
- geometrisch [
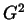 -Kontinuität]:
-Kontinuität]:
Neben 1. und 2.2. muss
gelten:
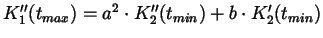 , mit (
, mit (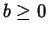 ).
).
Der Parameter 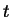 hat bei Bézier-Kurven und den beiden folgenden
Approximationsverfahren keine Auswirkung auf Tangentenrichtung und
Krümmung der Kurve. Der Betrag des Tangentenvektors und des
Krümmungsvektors sind aber parameterabhängig.
hat bei Bézier-Kurven und den beiden folgenden
Approximationsverfahren keine Auswirkung auf Tangentenrichtung und
Krümmung der Kurve. Der Betrag des Tangentenvektors und des
Krümmungsvektors sind aber parameterabhängig.
Bézier-Kontinuitätsbedingungen
[ Java-Applet starten |
Hinweis: Applet zur
Darstellung von zwei verbundener Bézier-Kurven, um die Auswirkung
der verschiedenen Übergangsbedingungen zu testen.]
Java-Applet starten |
Hinweis: Applet zur
Darstellung von zwei verbundener Bézier-Kurven, um die Auswirkung
der verschiedenen Übergangsbedingungen zu testen.]




 Java-Applet starten |
Hinweis: Applet zur
Darstellung von zwei verbundener Bézier-Kurven, um die Auswirkung
der verschiedenen Übergangsbedingungen zu testen.]
Java-Applet starten |
Hinweis: Applet zur
Darstellung von zwei verbundener Bézier-Kurven, um die Auswirkung
der verschiedenen Übergangsbedingungen zu testen.]


