Die eben beschriebene Methodik wird nun erweitert für die
Interpolation durch drei Stützpunkte und entsprechend berechnet
man zwei Kubische Spline-Kurven- segmente. Dabei beschreiben
jeweils zwei benachbarte Stützpunktpaare ein Kubisches
Spline-Kurvensegment. Wie immer in diesem Kapitel soll die
Ableitung am ersten und letzten Stützpunkt als
Randbedingungen vorgegeben sein. Die Gleichung
für das zweite Kurvensegment lautet:
Der Parameter 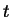 im zweiten Kurvensegment:
im zweiten Kurvensegment:
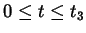 Bei nur einem Kurvensegment waren die beiden
Ableitungen an den Stützpunkten
Bei nur einem Kurvensegment waren die beiden
Ableitungen an den Stützpunkten 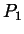 und
und 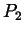 als
Randbedingung vorgegeben. Bei drei Stützpunkten sind die
Ableitungen an den Stützpunkten
als
Randbedingung vorgegeben. Bei drei Stützpunkten sind die
Ableitungen an den Stützpunkten 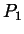 und
und 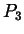 vorgegeben.
Gesucht ist jetzt die Ableitung an der Segmentgrenze, also am
Stützpunkt
vorgegeben.
Gesucht ist jetzt die Ableitung an der Segmentgrenze, also am
Stützpunkt 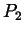 . Es soll nun die unbekannte Tangente
. Es soll nun die unbekannte Tangente 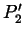 bestimmt werden, so dass Krümmungskontinuität über die
Segmentgrenze hinweg gewährleistet ist. Dazu muss folgende
Bedingung erfüllt sein:
bestimmt werden, so dass Krümmungskontinuität über die
Segmentgrenze hinweg gewährleistet ist. Dazu muss folgende
Bedingung erfüllt sein:
(im ersten Segment) (im zweiten Segment)
Die zweite Ableitung der Kurvengleichung
(2.1) ist:
| | |
|
|
|
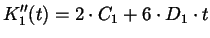 |
|
|
(2.11) |
Am Ende des ersten Spline-Kurvensegments ist:
Am Anfang des zweiten Spline-Kurvensegments ist:
Gleichsetzen von (2.12) und (2.13) ergibt:
| |
|
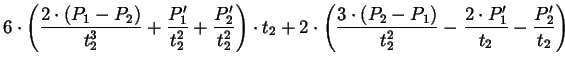 |
|
| |
|
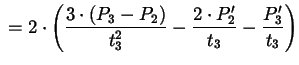 |
(2.14) |
Die Gleichung (2.14) kann nach dem gesuchten 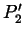 aufgelöst werden und ergibt:
aufgelöst werden und ergibt:
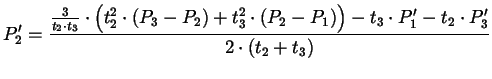 |
|
|
(2.15) |
So kann also 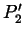 berechnet werden bei einer Kubischen
Spline-Kurve durch drei Stützpunkte. Hat man
berechnet werden bei einer Kubischen
Spline-Kurve durch drei Stützpunkte. Hat man 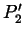 , können die
Koeffizienten
, können die
Koeffizienten 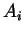 ,
, 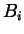 ,
, 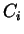 und
und 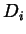 für die beiden
Kurvensegmente
für die beiden
Kurvensegmente 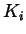 (
(
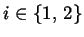 ) mit Hilfe der
Gleichungen (2.10) und (2.9) berechnet werden.
) mit Hilfe der
Gleichungen (2.10) und (2.9) berechnet werden.






