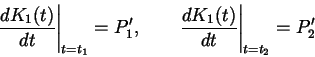Ein
Kubisches Spline-Kurvensegment durch zwei
Stützpunkte wird definiert durch die
vektorwertige parametrische Gleichung:
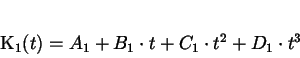 |
(2.1) |
Der Index 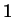 bei den Koeffizienten
bei den Koeffizienten 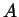 ,
, 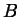 ,
,
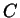 und
und 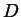 bedeutet, dass diese Koeffizienten zum ersten
Kurvensegment gehören. Der Parameter
bedeutet, dass diese Koeffizienten zum ersten
Kurvensegment gehören. Der Parameter 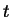 :
:
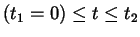 Die Randbedingungen für das erste bzw. hier nur ein Kurvensegment
sind:
Die Randbedingungen für das erste bzw. hier nur ein Kurvensegment
sind:
-
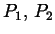 : Ortsvektoren der Stützpunkte
: Ortsvektoren der Stützpunkte
-
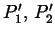 : Kurvenableitungen nach dem Parameter
: Kurvenableitungen nach dem Parameter 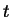 an
den Stützpunkten
an
den Stützpunkten 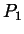 bzw.
bzw. 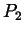
Siehe auch Java-Applet 2.1. Aus den
Randbedingungen ergeben sich die
Koeffizienten 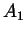 ,
, 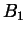 ,
, 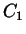 und
und 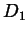 .
.
Java-Applet 2.1:
Die Randbedingungen bei einem Kubischen Spline-Kurvensegment
|
|
Die erste Ableitung des ersten
Kurvensegments nach dem Parameter 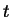 ist:
ist:
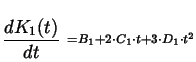 |
(2.2) |
Im Fall eines Kurvensegments ergeben sich aus den Randbedingungen:
(Die beiden gegebenen Stützpunkte sollen interpoliert
werden.)
(Am ersten und letzten Stützpunkt sind die Tangenten, also
Ableitungen, vorgegeben.)
Aus der Kurvengleichung (2.1) und der ersten Ableitung
(2.2) folgen die vier Koeffizienten:
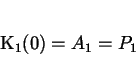 |
(2.3) |
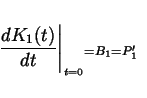 |
(2.4) |
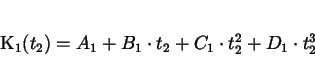 |
(2.5) |
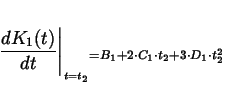 |
(2.6) |
Aus (2.5) und (2.6) ergeben sich:
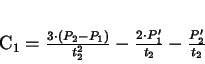 |
(2.7) |
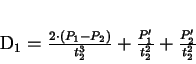 |
(2.8) |
Die Koeffizienten 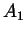 aus (2.3),
aus (2.3), 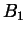 aus (2.4),
aus (2.4),
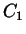 aus (2.7) und
aus (2.7) und 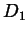 aus (2.8) in die
Kurvengleichung (2.1) eingesetzt ergeben ein Kubisches
Spline-Kurvensegment in Abhängigkeit von
aus (2.8) in die
Kurvengleichung (2.1) eingesetzt ergeben ein Kubisches
Spline-Kurvensegment in Abhängigkeit von
- den Randbedingungen
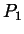 ,
, 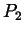 ,
, 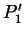 ,
, 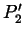
- dem Endparameterwert
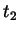
Also:
Zur Darstellung braucht man nur noch Informationen zur
Parametergrenze 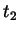 . Dieser Parameter bestimmt die Bogenlänge
des Kurvensegments vom Stützpunkt
. Dieser Parameter bestimmt die Bogenlänge
des Kurvensegments vom Stützpunkt 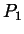 nach
nach 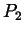 . Eine gute
Näherung ist:
. Eine gute
Näherung ist:
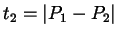 . Bisher wurde eine Kubische Spline-Kurve durch zwei
Stützpunkte und zwei gegebene Kurvenableitungen an diesen Punkten
beschrieben.
. Bisher wurde eine Kubische Spline-Kurve durch zwei
Stützpunkte und zwei gegebene Kurvenableitungen an diesen Punkten
beschrieben.