Zunächst wird die allgemeine Form des Verfahrens beschrieben. Der Parabelbogen aus
Java-Applet 2.3 durch die ersten drei Punkte in
Bezug auf das lokale Koordinatensystem dieser Punkte wird
folgendermaßen definiert:
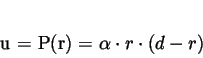 |
(2.21) |
mit
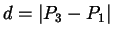
und
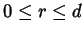
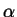 wird
so gewählt, daß die Parabel durch
wird
so gewählt, daß die Parabel durch 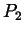 verläuft.
verläuft.
Java-Applet 2.3:
Parabolische Verbindungskurve: zwei Parabelbögen mit jeweils lokalem Koordinatensystem
|
|
Der zweite Parabelbogen durch 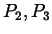 und
und 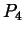 wird
analog definiert:
wird
analog definiert:
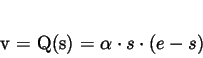 |
(2.22) |
mit
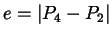
und
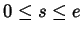
Die Parabolische Verbindungskurve wird nun zwischen 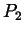 und
und
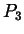 berechnet zu:
berechnet zu:
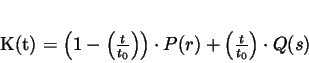 |
(2.23) |
mit
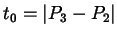
und
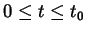 Der Parameter
Der Parameter 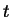 variiert auf der Sehne
variiert auf der Sehne
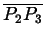 .
Die Koeffizienten
.
Die Koeffizienten
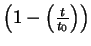 und
und
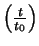 von
von 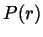 und
und 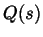 sind
Verbindungsfunktionen, die linear zwischen 0 und 1 bzw. 1 und 0
variieren (Wichtungsfunktionen, bzw. "blending functions").
Die soeben definierte Parabolische Verbindungskurve läuft von
sind
Verbindungsfunktionen, die linear zwischen 0 und 1 bzw. 1 und 0
variieren (Wichtungsfunktionen, bzw. "blending functions").
Die soeben definierte Parabolische Verbindungskurve läuft von
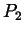 bis
bis 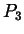 und liegt zwischen
und liegt zwischen 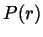 und
und 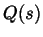 - an
ihrem Anfang dominieren die Eigenschaften von
- an
ihrem Anfang dominieren die Eigenschaften von 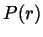 , am Ende die
von
, am Ende die
von 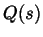 . Der Übergang ist linear.
. Der Übergang ist linear.
Im folgenden soll das eben beschriebene allgemeine Verfahren im
dreidimensionalen Raum umgesetzt werden.






